- On 2010-11-12
- By Edugain
Tessellations
A tessellation is simply is a set of figures that can cover a flat surface leaving no gaps. To explain it in simpler terms – consider the floor of your house. That is a flat surface - called a "plane" in mathematical terms. And you'll notice that the floor is covered with some tiles or marbles of different shapes. That is a good example of a "tessellation". The one difference here is that technically a plane is infinite in length and width so it's like a floor that goes on forever.
Of course, when we are talking about floors, the shapes used to cover it are mostly rectangles or squares (in fact, the word "tessellation" comes from the Latin word tessella - which means "small square"). The word “Tiling” is also commonly used to refer to "tessellations".
There are different kinds of tessellations – the ones of most interest are tessellations created using polygons. If you use only one kind of polygon to tile the entire plane - that's called a "Regular Tessellation"
Regular Tessellations
As it turns out, there are only three possible polygons that can be used here. There are only three rules to be followed when doing a "regular tessellation" of a plane
- The tessellation must cover a plane (or an infinite floor) without any gaps or any overlaps.
- All the tiles must be the same shape and size and must be regular polygons (that means all sides are the same length)
- Each vertex (the points where the corners of the tiles meet) should look the same
Of course, you would have guessed that one is a square. What are the other two? They are triangles and hexagons. Let me show you examples of these two here.

You may wonder why other shapes won't work. Let's try with pentagons and see what shape we come up with. You can see that there is a gap and that's not allowed.

So what's unique to those 3 shapes (triangle, square and hexagon)? As it turns out, the key here is that the internal angles of each of these three is an exact divisor of 360 (internal angle of triangle is 60, that of square is 90, and for a hexagon is 120). The mathematics to explain this is a little complicated, so we won't look at it here
Semi-Regular Tessellations
If you use a combination of more than one regular polygon to tile the plane, then it's called a "semi-regular" tessellation. If you look at the rules above, only rule 2 changes slightly for semi-regular tessellations. All the other rules are still the same.
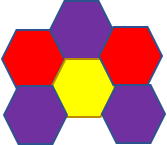
For example, you can use a combination of triangles and hexagons as follows to create a semi-regular tessellation. There are eight such tessellations possible

There are many other types of tessellations, like edge-to-edge tessellation (where the only condition is that adjacent tiles should share sides fully, not partially), and Penrose tilings. Each of these has many fascinating properties which mathematicians are continuing to study even today. Tessellations are also used in computer graphics where objects to be shown on screen are broken up like tessellations so that the computer can easily draw it on the monitor screen.
 Italy
Italy